Month: November 2018

The folly of absolute dichotomies

thegcatblog4 Comments

Divide and conquer (nothing)

Divisiveness is becoming quickly apparent as a plague on the modern era. The segregation and categorisation of people – whether politically, spiritually or morally justified – permeates throughout the human condition and in how we process the enormity of the Homo sapien population. The idea that the antithetic extremes form two discrete categories (for example, the waning centrist between ‘left’ vs. ‘right’ political perspectives) is widely employed in many aspects of the world.

But how pervasive is this pattern? How well can we summarise, divide and categorise people? For some things, this would appear innately very easy to do – one of the most commonly evoked divisions in people is that between men and women. But the increasingly charged debate around concepts of both gender and sex (and sexuality as a derivative, somewhat interrelated concept) highlights the inconsistency of this divide.

The ‘sex’ and ‘gender’ arguments

The most commonly used argument against ‘alternative’ concepts of either gender of sex – the binary states of a ‘man’ with a ‘male’ body and a ‘female’ with a ‘female’ body – is often based on some perception of “biologically reality.” As a (trainee) biologist, let me make this apparently clear that such confidence and clarity of “reality” in many, if not all, biological subdisciplines is absurd (e.g. “nature vs. nurture”). Biologists commonly acknowledge (and rely upon) the realisation that life in all of its constructs is unfathomably diverse, unique, and often difficult to categorise. Any impression of being able to do so is a part of the human limitation to process concepts without boundaries.

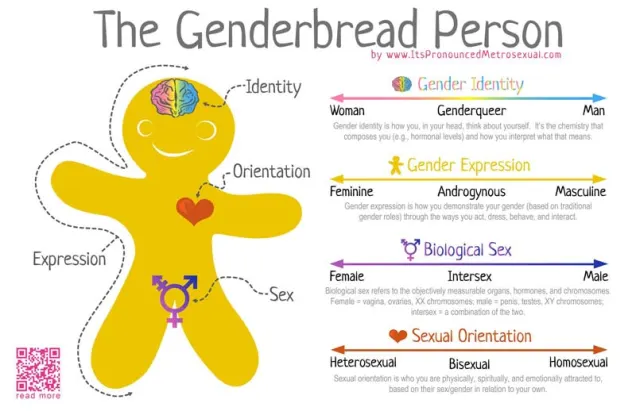
Genderbread-Person figure
A great example of the complex nature of human sex and gender. You’ll notice that each category is itself a spectrum: even Biological Sex is not a clearly binary system. In fact, even this representation likely simplifies the complexity of human identity and sexuality given that each category is only a single linear scale (e.g. pansexuality and asexuality aren’t on the Sexual Orientation gradient), but nevertheless is a good summary. Source: It’s Pronounced METROsexual.

Gender as a binary

In terms of gender identity, I think this is becoming (slowly) more accepted over time. That most people have a gender identity somewhere along a multidimensional spectrum is not, for many people, a huge logical leap. Trans people are not mentally ill, not all ‘men’ identify as ‘men’ and certainly not all ‘men’ identify as a ‘man’ under the same characteristics or expression. Human psychology is beautifully complex and to reduce people down to the most simplistic categories is, in my humble opinion, a travesty. The single-variable gender binary cannot encapsulate the full depth of any single person’s identity or personality, and this biologically makes sense.

Sex as a binary

As an extension of the gender debate, sex itself has often been relied upon as the last vestige of some kind of sexual binary. Even for those more supported of trans people, sex is often described as some concrete, biologically, genetically-encoded trait which conveniently falls into its own binary system. Thus, instead of a single binary, people are reduced down to a two-character matrix of sex and gender.

Gender and sex table.jpg
A representative table of the “2 Character Sex and Gender” composition. Although slightly better at allowing for complexity in people’s identities, having 2 binaries instead of 1 doesn’t encapsulate the full breadth of diversity in either sex or gender.

However, the genetics of the definition and expression of sex is in itself a complex network of the expression of different genes and the presence of different chromosomes. Although high-school level biology teaches us that men are XY and women are XX genetically, individual genes within those chromosomes can alter the formation of different sexual organs and the development of a person. Furthermore, additional X or Y chromosomes can further alter the way sexual development occurs in people. Many people who fall in between the two ends of the gender spectrum of Male and Female identify as ‘intersex’.

DSD types table.jpg
A list of some of the known types of ‘Disorders of Sex Development’ (DSDs) which can lead to non-binary sex development in many different ways. Within these categories, there may be multiple genetic mechanisms (e.g. specific mutations) underlying the symptoms. It’s also important to note that while DSD medically describes the conditions of many people, it can be offensive/inappropriate to many intersex people (‘disorder’ can be a heavy word). Source: El-Sherbiny (2013).

You might be under the impression that these are rare ‘genetic disorders’, and don’t count as “real people” (decidedly not my words). But the reality is that intersex people are relatively common throughout the world, and occur roughly as frequently as true redheads or green eyes. Thus, the idea that excluding intersex people from the rest of societal definitions has very little merit, especially from a scientific point of view. Instead, allowing our definitions of both sex and gender to be broad and flexible allows us to incorporate the biological reality of the immense diversity of the world, even just within our own species.

Absolute species concepts

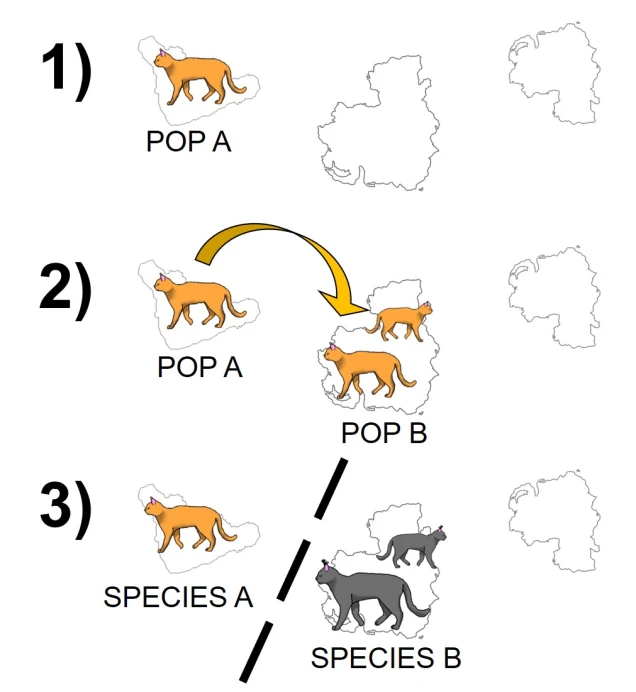
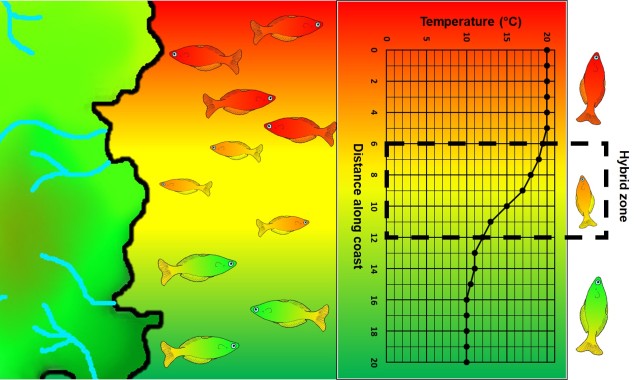
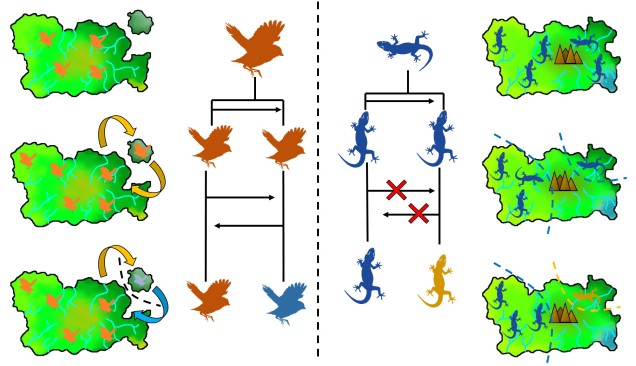
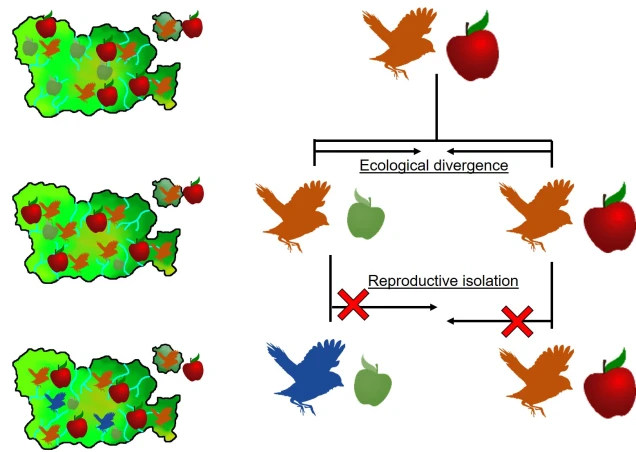
Speaking of species, and relating this paradigm of dichotomy to potentially less politically charged concepts, species themselves are a natural example on the inaccuracy of absolutism. This idea is not a new one, either within The G-CAT or within the broad literature, and species identity has long been regarded as a hive of grey areas. The sheer number of ways a group of organisms can be divided into species (or not, as the case may be) lends to the idea that simplified definitions of what something is or is not will rarely be as accurate as we hope. Even the most commonly employed of characteristics – such as those of the Biological Species Concept – cannot be applied to a number of biological systems such as asexually-reproducing species or complex cases of isolation.

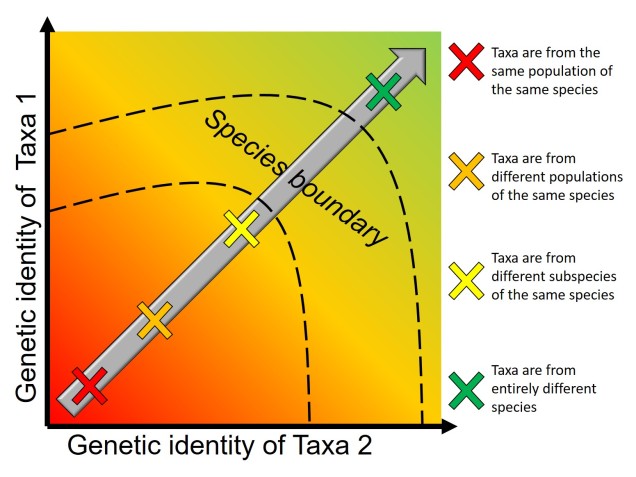
Speciation continuum figure
A figure describing the ‘speciation continuum’ from a previous post on The G-CAT. Now imagine that each Species Concept has it’s own vague species boundary (dotted line): draw 30 of them over the top of one another, and try to pick the exact cut-off between the red and green areas. Even using the imagination, this would be difficult.

The diversity of Life

Anyone who argues a biological basis for these concepts is taking the good name of biological science hostage. Diversity underpins the most core aspects of biology (e.g. evolution, communities and ecosystems, medicine) and is a real attribute of living in a complicated world. Downscaling and simplifying the world to the ‘black’ and the ‘white’ discredits the wonder of biology, and acknowledging the ‘outliers’ (especially those that are not actually so far outside the boxes we have drawn) of any trends we may observe in nature is important to understand the complexity of life on Earth. Even if individual components of this post seem debatable to you: always remember that life is infinitely more complex and colourful than we can even imagine, and all of that is underpinned by diversity in one form or another.

Bringing alleles back together: applications of coalescent theory

thegcatblog7 Comments

Coalescent theory

A recurring analytical method, both within The G-CAT and the broader ecological genetic literature, is based on coalescent theory. This is based on the mathematical notion that mutations within genes (leading to new alleles) can be traced backwards in time, to the point where the mutation initially occurred. Given that this is a retrospective, instead of describing these mutation moments as ‘divergence’ events (as would be typical for phylogenetics), these appear as moments where mutations come back together i.e. coalesce.

There are a number of applications of coalescent theory, and it is particularly fitting process for understanding the demographic (neutral) history of populations and species.

Mathematics of the coalescent

Before we can explore the multitude of applications of the coalescent, we need to understand the fundamental underlying model. The initial coalescent model was described in the 1980s, built upon by a number of different ecologists, geneticists and mathematicians. However, John Kingman is often attributed with the formation of the original coalescent model, and the Kingman’s coalescent is considered the most basic, primal form of the coalescent model.

From a mathematical perspective, the coalescent model is actually (relatively) simple. If we sampled a single gene from two different individuals (for simplicity’s sake, we’ll say they are haploid and only have one copy per gene), we can statistically measure the probability of these alleles merging back in time (coalescing) at any given generation. This is the same probability that the two samples share an ancestor (think of a much, much shorter version of sharing an evolutionary ancestor with a chimpanzee).

Normally, if we were trying to pick the parents of our two samples, the number of potential parents would be the size of the ancestral population (since any individual in the previous generation has equal probability of being their parent). But from a genetic perspective, this is based on the genetic (effective) population size (Ne), multiplied by 2 as each individual carries two copies per gene (one paternal and one maternal). Therefore, the number of potential parents is 2Ne.

Constant Ne and coalescent prob
A graph of the probability of a coalescent event (i.e. two alleles sharing an ancestor) in the immediately preceding generation (i.e. parents) relatively to the size of the population. As one might expect, with larger population sizes there is low chance of sharing an ancestor in the immediately prior generation, as the pool of ‘potential parents’ increases.

If we have an idealistic population, with large Ne, random mating and no natural selection on our alleles, the probability that their ancestor is in this immediate generation prior (i.e. share a parent) is 1/(2Ne). Inversely, the probability they don’t share a parent is 1 − 1/(2Ne). If we add a temporal component (i.e. number of generations), we can expand this to include the probability of how many generations it would take for our alleles to coalesce as (1 – (1/2Ne))t-1 x 1/2Ne.

Variable Ne and coalescent probs
The probability of two alleles sharing a coalescent event back in time under different population sizes. Similar to above, there is a higher probability of an earlier coalescent event in smaller populations as the reduced number of ancestors means that alleles are more likely to ‘share’ an ancestor. However, over time this pattern consistently decreases under all population size scenarios.

Although this might seem mathematically complicated, the coalescent model provides us with a scenario of how we would expect different mutations to coalesce back in time if those idealistic scenarios are true. However, biology is rarely convenient and it’s unlikely that our study populations follow these patterns perfectly. By studying how our empirical data varies from the expectations, however, allows us to infer some interesting things about the history of populations and species.

Testing changes in Ne and bottlenecks

One of the more common applications of the coalescent is in determining historical changes in the effective population size of species, particularly in trying to detect genetic bottleneck events. This is based on the idea that alleles are likely to coalesce at different rates under scenarios of genetic bottlenecks, as the reduced number of individuals (and also genetic diversity) associated with bottlenecks changes the frequency of alleles and coalescence rates.

For a set of k different alleles, the rate of coalescence is determined as k(k – 1)/4Ne. Thus, the coalescence rate is intrinsically linked to the number of genetic variants available: Ne. During genetic bottlenecks, the severely reduced Ne gives the appearance of coalescence rate speeding up. This is because alleles which are culled during the bottleneck event by genetic drift causes only a few (usually common) alleles to make it through the bottleneck, with the mutation and spread of these alleles after the bottleneck. This can be a little hard to think of, so the diagram below demonstrates how this appears.

Bottleneck test figure.jpg
A diagram of how the coalescent can be used to detect bottlenecks in a single population (centre). In this example, we have contemporary population in which we are tracing the coalescence of two main alleles (red and green, respectively). Each circle represents a single individual (we are assuming only one allele per individual for simplicity, but for most animals there are up to two).  Looking forward in time, you’ll notice that some red alleles go extinct just before the bottleneck: they are lost during the reduction in Ne. Because of this, if we measure the rate of coalescence (right), it is much higher during the bottleneck than before or after it. Another way this could be visualised is to generate gene trees for the alleles (left): populations that underwent a bottleneck will typically have many shorter branches and a long root, as many branches will be ‘lost’ by extinction (the dashed lines, which are not normally seen in a tree).

This makes sense from theoretical perspective as well, since strong genetic bottlenecks means that most alleles are lost. Thus, the alleles that we do have are much more likely to coalesce shortly after the bottleneck, with very few alleles that coalesce before the bottleneck event. These alleles are ones that have managed to survive the purge of the bottleneck, and are often few compared to the overarching patterns across the genome.

Testing migration (gene flow) across lineages

Another demographic factor we may wish to test is whether gene flow has occurred across our populations historically. Although there are plenty of allele frequency methods that can estimate contemporary gene flow (i.e. within a few generations), coalescent analyses can detect patterns of gene flow reaching further back in time.

In simple terms, this is based on the idea that if gene flow has occurred across populations, then some alleles will have been transferred from one population to another. Because of this, we would expect that transferred alleles coalesce with alleles of the source population more recently than the divergence time of the two populations. Thus, models that include a migration rate often add it as a parameter specifying the probability than any given allele coalesces with an allele in another population or species (the backwards version of a migration or introgression event). Again, this might be difficult to conceptualise so there’s a handy diagram below.

Migration rate test figure
A similar model of coalescence as above, but testing for migration rate (gene flow) in two recently diverged populations (right). In this example, when we trace two alleles (red and green) back in time, we notice that some individuals in Population 1 coalesce more recently with individuals of Population 2 than other individuals of Population 1 (e.g. for the red allele), and vice versa for the green allele. This can also be represented with gene trees (left), with dashed lines representing individuals from Population 2 and whole lines representing individuals from Population 1. This incomplete split between the two populations is the result of migration transferring genes from one population to the other after their initial divergence (also called ‘introgression’ or ‘horizontal gene transfer’).

Testing divergence time

In a similar vein, the coalescent can also be used to test how long ago the two contemporary populations diverged. Similar to gene flow, this is often included as an additional parameter on top of the coalescent model in terms of the number of generations ago. To convert this to a meaningful time estimate (e.g. in terms of thousands or millions of years ago), we need to include a mutation rate (the number of mutations per base pair of sequence per generation) and a generation time for the study species (how many years apart different generations are: for humans, we would typically say ~20-30 years).

Divergence time test figure.jpg
An example of using the coalescent to test the divergence time between two populations, this time using three different alleles (red, green and yellow). Tracing back the coalescence of each alleles reveals different times (in terms of which generation the coalescence occurs in) depending on the allele (right). As above, we can look at this through gene trees (left), showing variation how far back the two populations (again indicated with bold and dashed lines respectively) split. The blue box indicates the range of times (i.e. a confidence interval) around which divergence occurred: with many more alleles, this can be more refined by using an ‘average’ and later related to time in years with a generation time.

 

The basic model of testing divergence time with the coalescent is relatively simple, and not all that different to phylogenetic methods. Where in phylogenetics we relate the length of the different branches in the tree to the amount of time that has occurred since the divergence of those branches, with the coalescent we base these on coalescent events, with more coalescent events occurring around the time of divergence. One important difference in the two methods is that coalescent events might not directly coincide with divergence time (in fact, we expect many do not) as some alleles will separate prior to divergence, and some will lag behind and start to diverge after the divergence event.

The complex nature of the coalescent

While each of these individual concepts may seem (depending on how well you handle maths!) relatively simple, one critical issue is the interactive nature of the different factors. Gene flow, divergence time and population size changes will all simultaneously impact the distribution and frequency of alleles and thus the coalescent method. Because of this, we often use complex programs to employ the coalescent which tests and balances the relative contributions of each of these factors to some extent. Although the coalescent is a complex beast, improvements in the methodology and the programs that use it will continue to improve our ability to infer evolutionary history with coalescent theory.

The space for species: how spatial aspects influence speciation

thegcatblog2 Comments

Spatial and temporal factors of speciation

The processes driving genetic differentiation, and the progressive development of populations along the speciation continuum, are complex in nature and influenced by a number of factors. Generally, on The G-CAT we have considered the temporal aspects of these factors: how time much time is needed for genetic differentiation, how this might not be consistent across different populations or taxa, and how a history of environmental changes affect the evolution of populations and species. We’ve also touched on the spatial aspects of speciation and genetic differentiation before, but in significantly less detail.

To expand on this, we’re going to look at a few different models of how the spatial distribution of populations influences their divergence, and particularly how these factor into different processes of speciation.

What comes first, ecological or genetic divergence?

One key paradigm in understanding speciation is somewhat an analogy to the “chicken and the egg scenario”, albeit with ecological vs. genetic divergence. This concept is based on the idea that two aspects are key for determining the formation of new species: genetic differentiation of the populations in question, and ecological (or adaptive) changes that provide new ecological niches for species to inhabit. Without both, we might have new morphotypes or ecotypes of a singular species (in the case of ecological divergence without strong genetic divergence) or cryptic species (genetically distinct but ecologically identical species).

The order of these two processes have been in debate for some time, and different aspects of species and the environment can influence how (or if) these processes occur.

Different spatial models of speciation

Generally, when we consider the spatial models for speciation we divide these into distinct categories based on the physical distance of populations from one another. Although there is naturally a lot of grey area (as there is with almost everything in biological science), these broad concepts help us to define and determine how speciation is occurring in the wild.

Allopatric speciation

The simplest model is one we have described before called “allopatry”. In allopatry, populations are distributed distantly from one another, so that there are separated and isolated. A common way to imagine this is islands of populations separated by ocean of unsuitable habitat.

Allopatric speciation is considered one of the simplest and oldest models of speciation as the process is relatively straightforward. Geographic isolation of populations separates them from one another, meaning that gene flow is completely stopped and each population can evolve independently. Small changes in the genes of each population over time (e.g. due to different natural selection pressures) cause these populations to gradually diverge: eventually, this divergence will reach a point where the two populations would not be compatible (i.e. are reproductively isolated) and thus considered separate species.

Allopatry_example
The standard model of allopatric speciation, following an island model. 1) We start with a single population occupying a single island.  2) A rare dispersal event pushes some individuals onto a new island, forming a second population. Note that this doesn’t happen often enough to allow for consistent gene flow (i.e. the island was only colonised once). 3) Over time, these populations may accumulate independent genetic and ecological changes due to both natural selection and drift, and when they become so different that they are reproductively isolated they can be considered separate species.

Although relatively straightforward, one complex issue of allopatric speciation is providing evidence that hybridisation couldn’t happen if they reconnected, or if populations could be considered separate species if they could hybridise, but only under forced conditions (i.e. it is highly unlikely that the two ‘species’ would interact outside of experimental conditions).

Parapatric and peripatric speciation

A step closer in bringing populations geographically together in speciation is “parapatry” and “peripatry”. Parapatric populations are often geographically close together but not overlapping: generally, the edges of their distributions are touching but do not overlap one another. A good analogy would be to think of countries that share a common border. Parapatry can occur when a species is distributed across a broad area, but some form of narrow barrier cleaves the distribution in two: this can be the case across particular environmental gradients where two extremes are preferred over the middle.

The main difference between paraptry and allopatry is the allowance of a ‘hybrid zone’. This is the region between the two populations which may not be a complete isolating barrier (unlike the space between allopatric populations). The strength of the barrier (and thus the amount of hybridisation and gene flow across the two populations) is often determined by the strength of the selective pressure (e.g. how unfit hybrids are). Paraptry is expected to reduce the rate and likelihood of speciation occurring as some (even if reduced) gene flow across populations is reduces the amount of genetic differentiation between those populations: however, speciation can still occur.

Parapatric speciation across a thermocline.jpg
An example of parapatric species across an environment gradient (in this case, a temperature gradient along the ocean coastline). Left: We have two main species (red and green fish) which are adapted to either hotter or colder temperatures (red and green in the gradient), respectively. A small zone of overlap exists where hybrid fish (yellow) occur due to intermediate temperature. Right: How the temperature varies across the system, forming a steep gradient between hot and cold waters.

Related to this are peripatric populations. This differs from parapatry only slightly in that one population is an original ‘source’ population and the other is a ‘peripheral’ population. This can happen from a new population becoming founded from the source by a rare dispersal event, generating a new (but isolated) population which may diverge independently of the source. Alternatively, peripatric populations can be formed when the broad, original distribution of the species is reduced during a population contraction, and a remnant piece of the distribution becomes fragmented and ‘left behind’ in the process, isolated from the main body. Speciation can occur following similar processes of allopatric speciation if gene flow is entirely interrupted or paraptric if it is significantly reduced but still present.

Peripatric distributions.jpg
The two main ways peripatric species can form. Left: The dispersal method. In this example, there is a central ‘source’ population (orange birds on the main island), which holds most of the distribution. However, occasionally (more frequently than in the allopatric example above) birds can disperse over to the smaller island, forming a (mostly) independent secondary population. If the gene flow between this population and the central population doesn’t overwhelm the divergence between the two populations (due to selection and drift), then a new species (blue birds) can form despite the gene flow. Right: The range contraction method. In this example, we start with a single widespread population (blue lizards) which has a rapid reduction in its range. However, during this contraction one population is separated from the main body (i.e. as a refugia), which may also be a precursor of peripatric speciation.

Sympatric (ecological) speciation

On the other end of the distribution spectrum, the two diverging populations undergoing speciation may actually have completely overlapping distributions. In this case, we refer to these populations as “sympatric”, and the possibility of sympatric speciation has been a highly debated topic in evolutionary biology for some time. One central argument rears its head against the possibility of sympatric speciation, in that if populations are co-occurring but not yet independent species, then gene flow should (theoretically) occur across the populations and prevent divergence.

It is in sympatric speciation that we see the opposite order of ecological and genetic divergence happen. Because of this, the process is often referred to as “ecological speciation”, where individual populations adapt to different niches within the same area, isolating themselves from one another by limiting their occurrence and tolerances. As the two populations are restricted from one another by some kind of ecological constraint, they genetically diverge over time and speciation can occur.

This can be tricky to visualise, so let’s invent an example. Say we have a tropical island, which is occupied by one bird species. This bird prefers to eat the large native fruit of the island, although there is another fruit tree which produces smaller fruits. However, there’s only so much space and eventually there are too many birds for the number of large fruit trees available. So, some birds are pushed to eat the smaller fruit, and adapt to a different diet, changing physiology over time to better acquire their new food and obtain nutrients. This shift in ecological niche causes the two populations to become genetically separated as small-fruit-eating-birds interact more with other small-fruit-eating-birds than large-fruit-eating-birds. Over time, these divergences in genetics and ecology causes the two populations to form reproductively isolated species despite occupying the same island.

Ecological sympatric speciation
A diagram of the ecological speciation example given above. Note that ecological divergence occurs first, with some birds of the original species shifting to the new food source (‘ecological niche’) which then leads to speciation. An important requirement for this is that gene flow is somehow (even if not totally) impeded by the ecological divergence: this could be due to birds preferring to mate exclusively with other birds that share the same food type; different breeding seasons associated with food resources; or other isolating mechanisms.

Although this might sound like a simplified example (and it is, no doubt) of sympatric speciation, it’s a basic summary of how we ended up with so many species of Darwin’s finches (and why they are a great model for the process of evolution by natural selection).

The complexity of speciation

As you can see, the processes and context driving speciation are complex to unravel and many factors play a role in the transition from population to species. Understanding the factors that drive the formation of new species is critical to understanding not just how evolution works, but also in how new diversity is generated and maintained across the globe (and how that might change in the future).