fitness

The genetics of adaptation

Adaptation and evolution by natural selection remains one of the most significant research questions in many disciplines of biology, and this is undoubtedly true for molecular ecology. While traditional evolutionary studies have been based on the physiological aspects of organisms and how this relates to their evolution, such as how these traits improve their fitness, the genetic component of adaptation is still somewhat elusive for many species and traits.

Hunting for adaptive genes in the genome

We’ve previously looked at the two main categories of genetic variation: neutral and adaptive. Although we’ve focused predominantly on the neutral components of the genome, and the types of questions about demographic history, geographic influences and the effect of genetic drift, they cannot tell us (directly) about the process of adaptation and natural selective changes in species. To look at this area, we’d have to focus on adaptive variation instead; that is, genes (or other related genetic markers) which directly influence the ability of a species to adapt and evolve. These are directly under natural selection, either positively (‘selected for’) or negatively (‘selected against’).

Given how complex organisms, the environment and genomes can be, it can be difficult to determine exactly what is a real (i.e. strong) selective pressure, how this is influenced by the physical characteristics of the organism (the ‘phenotype’) and which genes are fundamental to the process (the ‘genotype’). Even determining the relevant genes can be difficult; how do we find the needle-like adaptive genes in a genomic haystack?

Magnifying glass figure — If only it were this easy.

There’s a variety of different methods we can use to find adaptive genetic variation, each with particular drawbacks and strengths. Many of these are based on tests of the frequency of alleles, rather than on the exact genetic changes themselves; adaptation works more often by favouring one variant over another rather than completely removing the less-adaptive variant (this would be called ‘fixation’). So measuring the frequency of different alleles is a central component of many analyses.

F_ST outlier tests

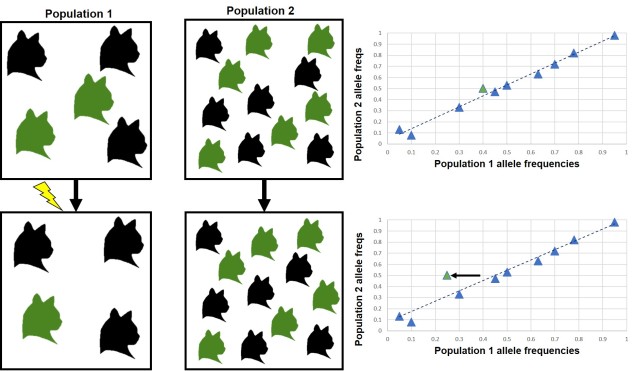
One of the most classical examples is called an ‘F_ST outlier test’. This can be a bit complicated without understanding what F_ST is actually measures: in short terms, it’s a statistical measure of ‘population differentiation due to genetic structure’. The F_ST value of one particular population can determine how genetically similar it is to another. An F_ST value of 1 implies that the two populations are as genetically different as they could possibly be, whilst an F_ST value of 0 implies that they are genetically identical populations.

Generally, F_ST reflects neutral genetic structure: it gives a background of how, on average, different are two populations. However, if we know what the average amount of genetic differentiation should be for a neutral DNA marker, then we would predict that adaptive markers are significantly different. This is because a gene under selection should be more directly pushed towards or away from one variant (allele) than another, and much more strongly than the neutral variation would predict. Thus, the alleles that are way more or less frequent than the average pattern we might assume are under selection. This is the basis of the F_ST outlier test; by comparing two or more populations (using F_ST), and looking at the distribution of allele frequencies, we can pick out a few alleles that vary from the average pattern and suggest that they are under selection (i.e. are adaptive).

There are a few significant drawbacks for F_ST outlier tests. One of the most major ones is that genetic drift can also produce a large number of outliers; in a small population, for example, one allele might be fixed (has a frequency of 1, with no alternative allele in the population) simply because there is not enough diversity or population size to sustain more alleles. Even if this particular allele was extremely detrimental, it’d still appear to be favoured by natural selection just because of drift.

Drift leading to outliers diagram — An example of genetic drift leading to outliers, featuring our friends the cat population. Top row: Two cat populations, one small (left; n = 5) and one large (middle, n = 12) show little genetic differentiation between them (right; each triangle represents a single gene or locus; the ‘colour’ gene is marked in green). The average (‘neutral’) pattern of differentiation is shown by the dashed line. Much like in our original example, one cat in the small population is horrifically struck by lightning and dies (RIP again). Now when we compare the frequency of the alleles of the two populations (bottom), we see that (because a green cat died), the ‘colour’ locus has shifted away from the general trend (right) and is now an outlier. Thus, genetic drift in the ‘colour’ gene gives the illusion of a selective loci (even though natural selection didn’t cause the change, since colour does not relate to how likely a cat is to be struck by lightning).

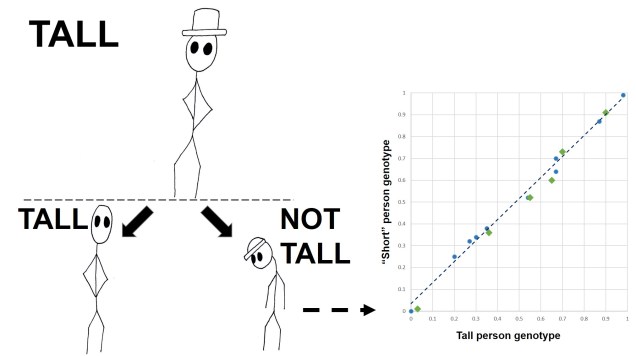
Secondly, the cut-off for a ‘significant’ vs. ‘relatively different but possibly not under selection’ can be a bit arbitrary; some genes that are under weak selection can go undetected. Furthermore, recent studies have shown a growing appreciation for polygenic adaptation, where tiny changes in allele frequencies of many different genes combine together to cause strong evolutionary changes. For example, despite the clear heritable nature of height (tall people often have tall children), there is no clear ‘height’ gene: instead, it appears that hundreds of genes are potentially very minor height contributors.

Polygenic height figure final — In this example, we have one tall parent (top) who produces two offspring; one who is tall (left) and one who isn’t (right). In order to understand what genetic factors are contributing to their height differences, we compare their genetics (right; each dot represents a single locus). Although there aren’t any particular loci that look massively different between the two, the cumulative effect of tiny differences (the green triangles) together make one person taller than the other. There are no clear outliers, but many (poly) different genes (genic) acting together.

Genotype-environment associations

To overcome these biases, sometimes we might take a more methodological approach called ‘genotype-environment association’. This analysis differs in that we select what we think our selective pressures are: often environmental characteristics such as rainfall, temperature, habitat type or altitude. We then take two types of measures per individual organism: the genotype, through DNA sequencing, and the relevant environmental values for that organisms’ location. We repeat this over the full distribution of the species, taking a good number of samples per population and making sure we capture the full variation in the environment. Then we perform a correlation-type analysis, which seeks to see if there’s a connection or trend between any particular alleles and any environmental variables. The most relevant variables are often pulled out of the environmental dataset and focused on to reduce noise in the data.

The main benefit of GEA over F_ST outlier tests is that it’s unlikely to be as strongly influenced by genetic drift. Unless (coincidentally) populations are drifting at the same genes in the same pattern as the environment, the analysis is unlikely to falsely pick it up. However, it can still be confounded by neutral population structure; if one population randomly has a lot of unique alleles or variation, and also occurs in a somewhat unique environment, it can bias the correlation. Furthermore, GEA is limited by the accuracy and relevance of the environmental variables chosen; if we pick only a few, or miss the most important ones for the species, we won’t be able to detect a large number of very relevant (and likely very selective) genes. This is a universal problem in model-based approaches and not just limited to GEA analysis.

New spells to find adaptive genes?

It seems likely that with increasing datasets and better analytical platforms, many more types of analysis will be developed to delve deeper into the adaptive aspects of the genome. With whole-genome sequencing starting to become a reality for non-model species, better annotation of current genomes and a steadily increasing database of functional genes, the ability of researchers to investigate evolution and adaptation at the genomic level is also increasing.

How random is evolution?

Often, we like to think of evolution fairly anthropomorphically; as if natural selection actively decides what is, and what isn’t, best for the evolution of a species (or population). Of course, there’s not some explicit Evolution God who decrees how a species should evolve, and in reality, evolution reflects a more probabilistic system. Traits that give a species a better chance of reproducing or surviving, and can be inherited by the offspring, will over time become more and more dominant within the species; contrastingly, traits that do the opposite will be ‘weeded out’ of the gene pool as maladaptive organisms die off or are outcompeted by more ‘fit’ individuals. The fitness value of a trait can be determined from how much the frequency of that trait varies over time.

So, if natural selection is just probabilistic, does this mean evolution is totally random? Is it just that traits are selected based on what just happens to survive and reproduce in nature, or are there more direct mechanisms involved? Well, it turns out both processes are important to some degree. But to get into it, we have to explain the difference between genetic drift and natural selection (we’re assuming here that our particular trait is genetically determined).

Allele frequency over time diagram — The (statistical) overview of natural selection. In this example, we have two different traits in a population; the blue X and the red O. Our starting population is 20 individuals (N), with 10 of each trait (a 1:1 ratio, or 50% frequency of each). We’re going to assume that, because the blue X is favoured by natural selection, it doubles in frequency each generation (i.e. one individual with the blue X has two offspring with one blue X each). The red O is neither here nor there and is stable over time (one red O produces one red O in the next generation). So, going from Gen 1 to Gen 2, we have twice as many blue Xs (Nt) as we did previously, changing the overall frequency of the traits (highlighted in yellow). Because populations probably don’t exponentially increase every generation, we’ll cut it back down to our original total of 20, but at the same ratios (Np). Over time, we can see that the population gradually accumulates more blue Xs relative to red Os, and by Gen 5 the red O is extinct. Thus, the **blue X has evolved!**

When we consider the genetic variation within a species to be our focal trait, we can tell that different parts of the genome might be more related with natural selection than others. This makes sense; some mutations in the genome will directly change a trait (like fur colour) which might have a selective benefit or detriment, while others might not change anything physically or change traits that are neither here-nor-there under natural selection (like nose shape in people, for example). We can distinguish between these two by talking about adaptive or neutral variation; adaptive variation has a direct link to natural selection whilst neutral variation is predominantly the product of genetic drift. Depending on our research questions, we might focus on one type of variation over the other, but both are important components of evolution as a whole.

Genetic drift

Genetic drift is considered the random, selectively ‘neutral’ changes in the frequencies of different traits (alleles) over time, due to completely random effects such as random mutations or random loss of alleles. This results in the neutral variation we can observe in the gene pool of the species. Changes in allele frequencies can happen due to entirely stochastic events. If, by chance, all of the individuals with the blue fur variant of a gene are struck by lightning and die, the blue fur allele would end up with a frequency of 0 i.e. go extinct. That’s not to say the blue fur ‘predisposed’ the individuals to be struck be lightning (we assume here, anyway), so it’s not like it was ‘targeted against’ by natural selection (see the bottom figure for this example).

Because neutral variation appears under a totally random, probabilistic model, the mathematical basis of it (such as the rate at which mutations appear) has been well documented and is the foundation of many of the statistical aspects of molecular ecology. Much of our ability to detect which genes are under selection is by seeing how much the frequencies of alleles of that gene vary from the neutral model: if one allele is way more frequent than you’d expect by random genetic drift, then you’d say that it’s likely being ‘pushed’ by something: natural selection.

Manhattan plot example — A Manhattan plot, which measures the level of genetic differentiation between two different groups across the genome. The x-axis shows the length of the genome, in this example colour-coded by the specific chromosome of the sequence, while the y-axis shows the level of differentiation between the two groups being studied. The dots represent certain spots (*loci,* singular locus) in the genome, with the level of differentiation (Fst) measured for that locus in one group vs that locus in the other group. The dotted line represents the ‘average differentiation’: i.e. how different you’d expect the two groups to be by chance. Anything about that line is significantly different between the two groups, either because of drift or natural selection. This plot has been slightly adapted from Axelsson *et al.* (2013), who were studying domestication in dogs by comparing the genetic architecture of wild wolves versus domestic dogs. In this example we can see that certain regions of the genome are clearly different between dogs and wolves (circled); when the authors looked at the genes within those blocks, they found that many were related to behavioural changes (nervous system), competitive breeding (sperm-egg recognition) and interestingly, starch digestion. This last category suggests that adaptation to an omnivorous diet (likely human food waste) was key in the domestication process.

Natural selection

Contrastingly to genetic drift, natural selection is when particular traits are directly favoured (or unfavoured) in the environmental context of the population; natural selection is very specific to both the actual trait and how the trait works. A trait is only selected for if it conveys some kind of fitness benefit to the individual; in evolutionary genetics terms, this means it allows the individual to have more offspring or to survive better (usually).

While this might be true for a trait in a certain environment, in another it might be irrelevant or even have the reverse effect. Let’s again consider white fur as our trait under selection. In an arctic environment, white fur might be selected for because it helps the animal to camouflage against the snow to avoid predators or catch prey (and therefore increase survivability). However, in a dense rainforest, white fur would stand out starkly against the shadowy greenery of the foliage and thus make the animal a target, making it more likely to be taken by a predator or avoided by prey (thus decreasing survivability). Thus, fitness is very context-specific.

Who wins? Drift or selection?

So, which is mightier, the pen (drift) or the sword (selection)? Well, it depends on a large number of different factors such as mutation rate, the importance of the trait under selection, and even the size of the population. This last one might seem a little different to the other two, but it’s critically important to which process governs the evolution of the species.

In very small populations, we expect genetic drift to be the stronger process. Natural selection is often comparatively weaker because small populations have less genetic variation for it to act upon; there are less choices for gene variants that might be more beneficial than others. In severe cases, many of the traits are probably very maladaptive, but there’s just no better variant to be selected for; look at the plethora of physiological problems in the cheetah for some examples.

Genetic drift, however, doesn’t really care if there’s “good” or “bad” variation, since it’s totally random. That said, it tends to be stronger in smaller populations because a small, random change in the number or frequency of alleles can have a huge effect on the overall gene pool. Let’s say you have 5 cats in your species; they’re nearly extinct, and probably have very low genetic diversity. If one cat suddenly dies, you’ve lost 20% of your species (and up to that percentage of your genetic variation). However, if you had 500 cats in your species, and one died, you’d lose only <0.2% of your genetic variation and the gene pool would barely even notice. The same applies to random mutations, or if one unlucky cat doesn’t get to breed because it can’t find a mate, or any other random, non-selective reason. One way we can think of this is as ‘random error’ with evolution; even a perfectly adapted organism might not pass on its genes if it is really unlucky. A bigger sample size (i.e. more individuals) means this will have less impact on the total dataset (i.e. the species), though.

Drift in small pops — The effect of genetic drift on small populations. In this example, we have two very similar populations of cats, each with three different alleles (black, blue and green) in similar frequencies across the populations. The major difference is the size of the population; the left is much smaller (5 cats) compared to the right (20 cats). If one cat randomly dies from a bolt of lightning (**RIP**), and assuming that the colour of the cat has no effect on the likelihood of being struck by lightning (i.e. is not under natural selection), then the outcome of this event is entirely due to genetic drift. In this case, the left population has lost 1/5th of its population size and 1/3rd of its total genetic diversity thanks to the death of the genetically unique blue cat (He will be missed) whereas the right population has only really lost 1/20th of its size and no changes in total diversity (it’ll recover).

Both genetic drift and natural selection are important components of evolution, and together shape the overall patterns of evolution for any given species on the planet. The two processes can even feed into one another; random mutations (drift) might become the genetic basis of new selective traits (natural selection) if the environment changes to suit the new variation. Therefore, to ignore one in favour of the other would fail to capture the full breadth of the processes which ultimately shape and determine the evolution of all species on Earth, and thus the formation of the diversity of life.